بعد 60 عاماً من فشل العلماء.. شخص هاوٍ يحل معضلة رياضية بسهولة

فاجأ عالم البيولوجيا أوبري دي غراي، الذي يسعى إلى مدِّ عمر الإنسان، خبراء الرياضيات بإعلانه التوصل إلى حلٍّ جديد للمعضلة الرياضية المعروفة باسم "هادويغر-نيلسون".

وبحسب صحيفة The Guardian البريطانية، تبدو هذه المعضلة بسيطة بشكل مخادع، ولكن على الرغم من بذل بعض المتخصصين سنوات في محاولات حلها، فإن إحراز التقدم في تلك المساعي قد توقَّف بعد فترة وجيزة من ظهور تلك المعضلة لأول مرة عام 1950.

إذ قال جيل كالاي، عالم الرياضيات بالجامعة العبرية في القدس: "حرفياً، هذا هو أول تقدم منذ 60 عاماً".

ونستعرض المشكلة كما يلي: تخيل مجموعة من النقاط تتصل ببعضها البعض عن طريق خطوط، يمكن لهذه النقاط أن تتخذ أيَّ شكل ممكن، لكن الشرط الوحيد، أن تكون الخطوط الواصلة بينها متساوية الطول.

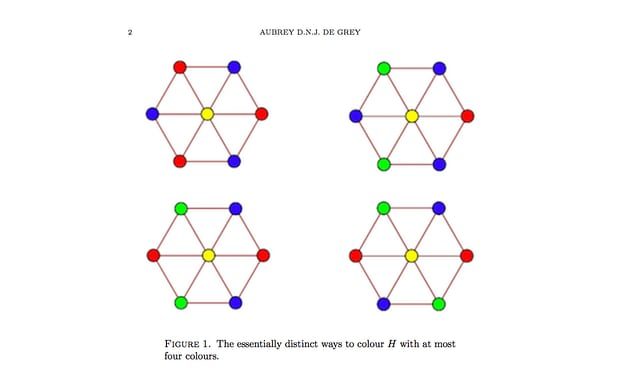
على سبيل المثال، في المربع لا يمكن توصيل القطر، فيما يمكن توصيل الحواف الخارجية. والآن، لوِّن جميع النقاط بحيث لا تأخذ نقطتان متصلتان نفس اللون. كم عدد الألوان المطلوبة؟

بالنسبة للمربع، ستكون الإجابة لونين فقط. ولكن تتمحور معضلة هادويغر-نيلسون حول معرفة الحد الأدنى من الألوان بالنسبة لأي شكل من الأشكال، حتى تلك الأشكال المسطَّحة التي تمتد عبر مستوى لا نهائي من الحجم.

أثبت علماء الرياضيات بعد فترة وجيزة من طرح المعضلة للمرة الأولى، أن عدد الألوان المطلوب ينحصر بين أربعة وسبعة ألوان، ولم يتم إحراز أي تقدم منذ ذلك الحين.

ومن خلال ورقة بحثية نُشرت على موقع Arxiv الإلكتروني للمسودات العلمية، بعنوانعدد ألوان الشكل المسطح 5 على الأقل، قلص دي غراي دائرة البحث.

وذكر عالم البيولوجيا أنه أُصيب بالدهشة لدى إحرازه هذا التقدم، بعد عمله على المعضلة لأسابيع قليلة فقط. وقال "لطالما حاولت حل المعضلات الرياضية المفتوحة طوال حياتي كبالغ، إلا أن هذه هي المرة الأولى التي أُحرز فيها تقدماً وأنا في الـ55 من عمري. من المحتمل جداً أن تكون هذه هي المرة الأخيرة أيضاً".

أسس دي غراي بحسب موقع Science Alert العلمي نموذجه على شكل أطلق عليه اسم "مُستدق موزر"، وهو شكل يتألف من سبع نقاط فقط، وأحد عشر ضلعاً، ويتطلب أربعة ألوان ليحقق شرط المعضلة.

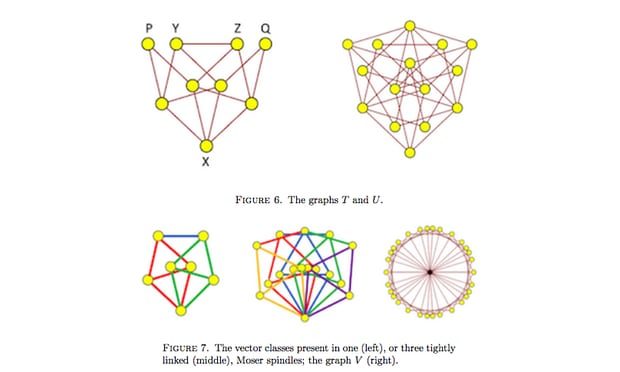
ولكن عند دمج هذا النموذج مع نموذج آخر لشكل ضخم يتكون من 20425 نقطة، تبيَّن أنه لا يمكن تلوينه باستخدام أربعة ألوان فقط. واستُخدم في ذلك حاسوب قوي لأغراض الأبحاث، الذي قام بتكرار النتائج على نموذج أصغر مكون من 1581 نقطة.

كما أشار تيموثي غاورز، أستاذ الرياضيات بجامعة كامبريدج إلى شهرة هذه المعضلة في علم الرياضيات التوافقية، ذلك القسم من الرياضيات الذي يركز على العد. وقال: "من غير المعتاد أن يتمكَّن رياضي هاوٍ من حلِّ معضلة شهيرة، بل إنه في كثير من الأحيان يشتهر الرياضيون الهواة في أوساط العامة لأسباب مختلفة تماماً".

فيما قال كالاي إن هذا التقدم قد حفَّز الآخرين في المجال على السعي لتطبيق استراتيجية مماثلة للتوصل إلى الحل الكامل